发表于 2024-09-08 更新于 2024-09-14 本文字数： 5.4k 阅读时长 ≈ 20 分钟

一阶低通滤波器

一阶低通滤波器（LPF）

https://blog.csdn.net/weixin_42887190/article/details/125749509

一阶低通滤波器允许低频信号通过，而抑制或衰减高频信号。这种滤波器通常由一个电阻和一个电容组成。

设计一阶低通滤波器时，需要确定两个关键参数：截止频率（fc）和滤波器的类型（这里是低通）。截止频率是滤波器开始显著衰减信号的频率。对于一阶低通滤波器，其传递函数中的时间常数（$\tau$）决定了截止频率。时间常数是电阻（R）和电容（C）的乘积：$\tau = R C$ 。

传递函数

一阶低通滤波器的传递函数通常表示为：（实际就是一个 一阶惯性环节 ）

\[ H(s) = \frac{1}{1 + s\tau} \]

其中，$s$ 是复频率（$j\omega$，$\omega$是角频率），$\tau$ 是时间常数。在频域中，这个传递函数可以用来预测滤波器对不同频率信号的响应。

”一阶低通数字滤波器“对应的物理电路模型是”一阶RC低通滤波电路“，电路如下图所示。

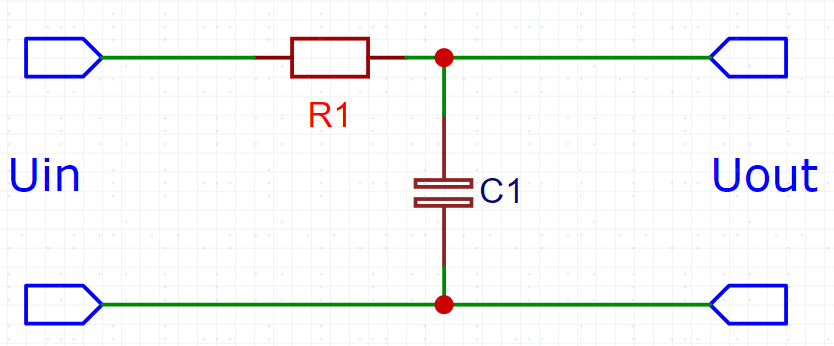
一阶RC低通滤波电路的传递函数

\[ G(s) = \frac{U_{out}}{U_{in}} = \frac{1}{1 + \tau s} = \frac{1}{1 + RCs} \]

其中：

$ s = j$ 为复频域变量
$ R $ 为电阻值
$ C $ 为电容值

截止频率公式

一阶惯性环节：

\[ L(j\omega) = \frac{1}{1 + j\omega \tau} \]

当 $\omega = \frac{1}{\tau}$ 时，$L(\omega) = -20 \lg(\sqrt{1+ \frac{1}{\tau^2} \cdot \tau^2}) \approx -3dB$，此时 $ = $ 为截止频率。

\[ f_c = \frac{\omega}{2\pi} = \frac{1}{2\pi \tau } \]

这个公式定义了滤波器的截止频率，即滤波器幅频响应曲线衰减-3dB时的频率。

当保持输入信号的幅度不变，改变频率使输出信号降至最大值的0.707倍，即用频响特性来表述即为-3dB点处即为截止频率，它是用来说明频率特性指标的一个特殊频率。

时域微分方程

\[ \tau \cdot y' + y = x \]

为了将这个连续时间滤波器离散化，我们可以使用一阶后向差分来近似其导数。在离散时间域中，导数可以用差分来表示。

现在，我们可以将连续时间滤波器的一阶导数用一阶后向差分来近似：

\[ s=\frac{1-z^{-1}}{T} \]

\[ y' = \frac{dy}{dt} \approx \frac{y[n] - y[n-1] }{T} \]

其中，$y[n]$ 是当前采样点的输出，$y[n-1]$ 是前一个采样点的输出，$T$ 是采样周期。

将这个近似代入连续时间滤波器的微分方程中，我们可以得到离散时间滤波器的一阶差分方程：

\[ y[n] = (1 - \frac{T}{T + \tau}) \cdot y[n-1] + \frac{T}{T + \tau} \cdot x[n] \]

令 $ a = $，则得到离散时间下的滤波器输出公式。

软件滤波器

\[ y[n] = (1 - a) \cdot y[n-1] + a \cdot x[n] \]

其中： - $ x[n] $ 为当前输入 - $ y[n-1] $ 为上一次的输出 - $ y[n] $ 为当前计算的输出 - $ a $ 为滤波系数，取值范围 $ 0 1 $

滤波系数 $ a $ 的计算公式

\[ a = \frac{T}{T + \tau} = \frac{1}{1 + \frac{\tau}{T}} = \frac{1}{1 + \frac{1}{T} \cdot \frac{1}{2\pi f_c}} = \frac{1}{1 + \frac{f_s}{2\pi f_c}} \]

其中： - $ T $ 为采样周期 - $ = RC $ 为时间常数 - $ f_s = $ 为采样频率 - $ f_c $ 为截止频率

在实际应用中，当采样频率远大于截止频率时（$ f_s >> f_c $），可以近似为：

\[ a \approx 2\pi \cdot \frac{f_c}{f_s} \]

代码

软件一阶低通滤波器

下面是一个，截止频率为50Hz，采样频率为70kHz的一阶低通滤波器的Python实现：

一阶低通滤波器的差分方程是：

\[ y[n] = \alpha \cdot x[n] + (1 - \alpha) \cdot y[n-1] \]

其中，$y[n]$ 是当前输出，$ x[n] $ 是当前输入，$ y[n-1] $ 是上一次输出，$ $ 是滤波器的系数。

系数α的计算公式为：

\[ \alpha = \frac{1}{1 + \tau \cdot f_s} \]

其中，$ $ 是滤波器的时间常数，与截止频率 $ f_c $ 的关系是 $ = $，而 $ f_s $ 是采样频率。

α的计算上面也讲了，等于：

\[ \alpha = \frac{1}{1 + \frac{f_s}{2\pi f_c}} \]

这里，$ f_c $ 是截止频率，设为50Hz；$ f_s $ 是采样频率，设为70kHz。

现在，我们可以根据这些公式来计算α，并使用Python实现滤波器。

import numpy as np  
import matplotlib.pyplot as plt  
  
class LowPassFilter:  
    def __init__(self, fc, fs):  
        """  
        初始化一阶低通滤波器  
  
        :param fc: 截止频率 (Hz)  
        :param fs: 采样频率 (Hz)  
        """  
        self.fc = fc  # 截止频率  
        self.fs = fs  # 采样频率  
        self.alpha = 1 / (1 + (fs / (2 * np.pi * fc)))  # 滤波系数
        self.y_prev = 0  # 上一次的输出值  
  
    def filter(self, x):  
        """  
        应用滤波器到单个输入样本  
  
        :param x: 当前输入样本  
        :return: 滤波后的输出样本  
        """  
        self.y = self.alpha * x + (1 - self.alpha) * self.y_prev  # 根据公式计算当前输出  
        self.y_prev = self.y  # 更新上一次输出为当前输出  
        return self.y  
  
# 使用示例  
fc = 50  # 截止频率50Hz  
fs = 70000  # 采样频率70kHz  
t = np.linspace(0, 3, int(fs), endpoint=False)  # 生成3秒的时间序列，样本数为fs  
  
# 创建一个直流信号，并添加50Hz纹波和噪声  
dc_signal = 5 * np.ones_like(t)  # 直流信号值，长度为t  
ripple = 0.5 * np.sin(2 * np.pi * 50 * t)  # 50Hz纹波  
noise = 0.2 * np.random.normal(0, 1, size=len(t))  # 随机噪声  
input_signal = dc_signal + ripple + noise  # 合成信号  
  
lpf = LowPassFilter(fc, fs)  
filtered_signal = np.array([lpf.filter(x) for x in input_signal])  # 应用滤波器到每个输入样本  
  
# 绘制以显示输入和滤波后的信号
plt.plot(t, input_signal, label='Input Signal')  
plt.plot(t, filtered_signal, label='Filtered Signal')  
plt.legend()  
plt.xlabel('Time (seconds)')  
plt.ylabel('Signal Value')  
plt.title('First-Order Low-Pass Filter Effect')  
plt.show()  
  
# 打印截止频率、采样频率和过滤器参数Alpha
print(f"Cut-off frequency: {fc} Hz")  
print(f"Sampling frequency: {fs} Hz")  
print(f"Filter parameter alpha: {lpf.alpha}")

运行结果：

1
2
3

Cut-off frequency: 50 Hz
Sampling frequency: 70000 Hz
Filter parameter alpha: 0.004467937448748722

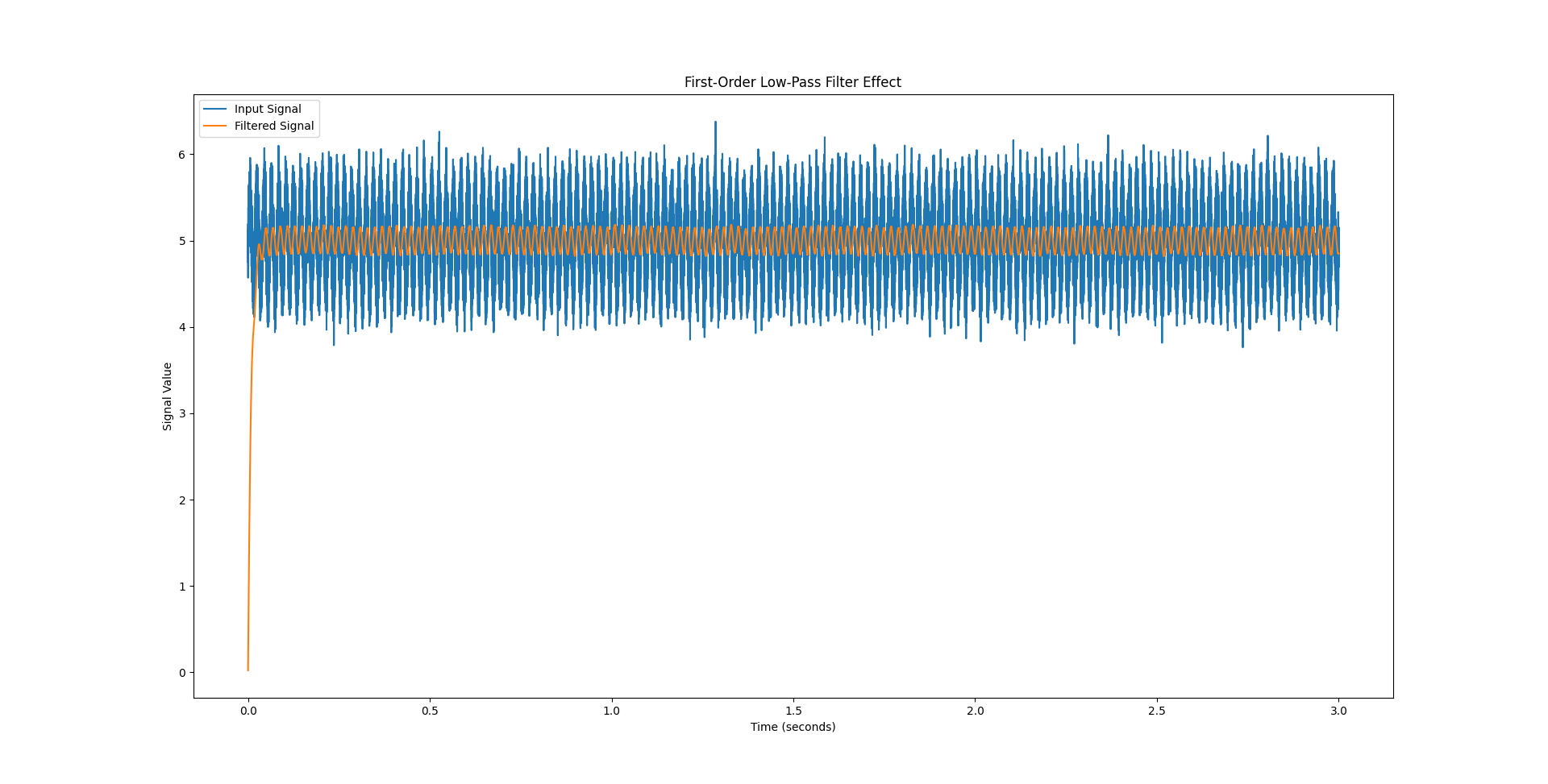
一阶低通滤波器，截止频率，Bode图

import numpy as np  
import matplotlib.pyplot as plt  
from scipy import signal  
  
# 设置截止频率和时间常数  
fc = 50  # 截止频率50Hz  
tau = 1 / (2 * np.pi * fc)  # 时间常数  
  
# 创建一阶低通滤波器  
num = [1]  # 分子系数  
den = [tau, 1]  # 分母系数  
system = signal.TransferFunction(num, den)  
  
# 生成频率响应数据  
omega, mag, phase = signal.bode(system)  
  
# 将频率从弧度/秒转换为Hz  
frequencies = omega / (2 * np.pi)  
  
# 找到-3dB点（即幅度衰减到0.707的点）  
cutoff_idx = np.argmin(np.abs(mag - (-3)))  # 找到最接近-3dB的索引  
cutoff_freq = frequencies[cutoff_idx]  # 对应的频率  
  
# 绘制幅频特性  
plt.figure(figsize=(8, 4))  
plt.plot(frequencies, mag)  
plt.title('Bode Plot - Magnitude')  
plt.xlabel('Frequency [Hz]')  
plt.ylabel('Magnitude [dB]')  
plt.grid(True)  
  
# 标记截止频率  
plt.axvline(x=cutoff_freq, color='r', linestyle='--', label='Cutoff Frequency')  
plt.annotate(f'Cutoff: {cutoff_freq:.2f} Hz', xy=(cutoff_freq, -3), xytext=(20, 20),  
             textcoords='offset points', arrowprops=dict(facecolor='black', shrink=0.05))  
plt.legend()  
  
plt.show()

运行结果：

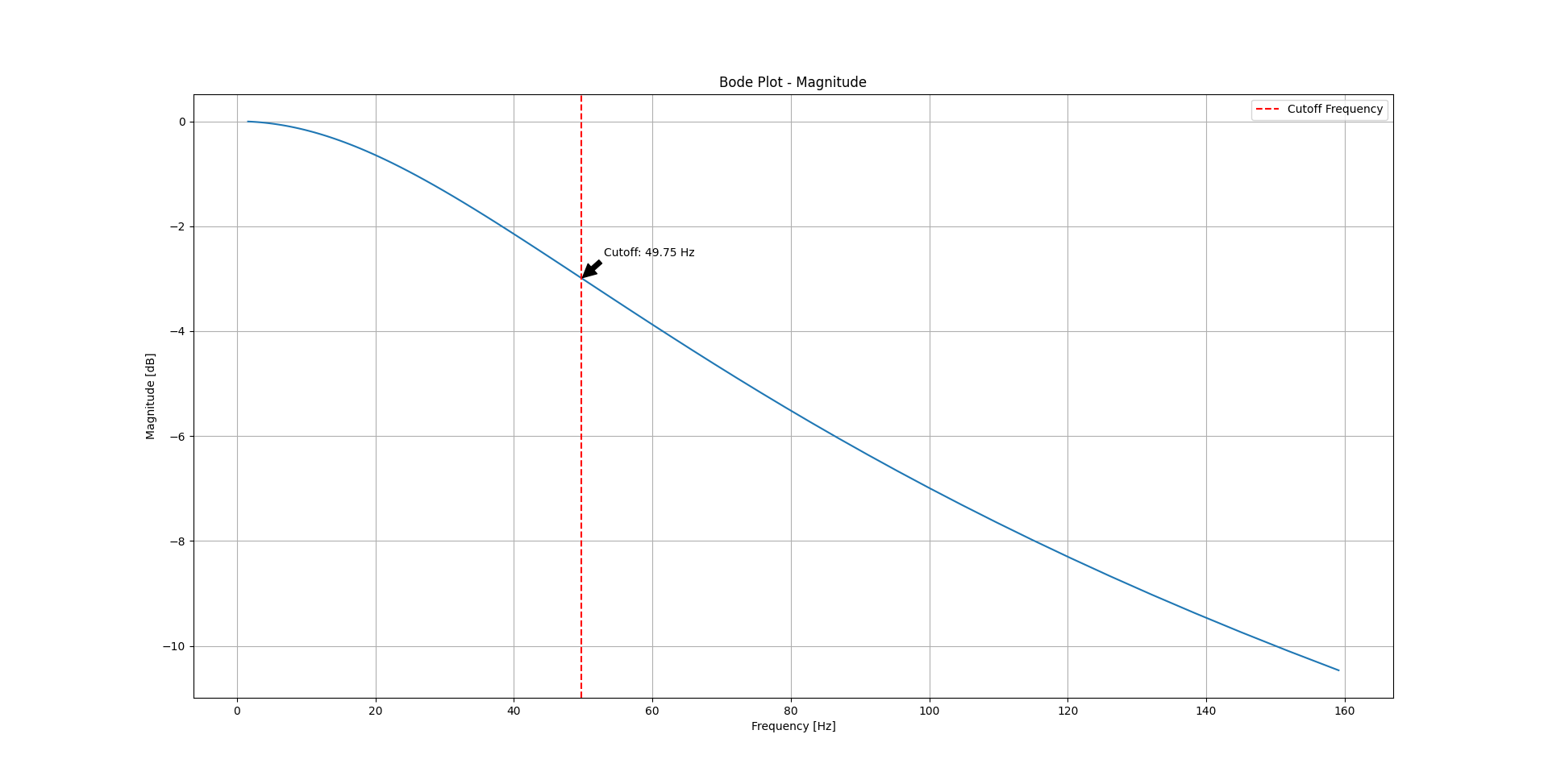
与python库对比

import numpy as np  
import matplotlib.pyplot as plt  
from scipy.signal import lfilter, butter  
  
# 设置参数  
fc = 10  # 截止频率10Hz  
fs = 70000  # 采样频率70kHz  
t = np.arange(0, 1, 1/fs)  # 1秒的时间数组  
  
# 创建输入信号  
dc_signal = 5 * np.ones_like(t)  # 直流信号  
ripple = 0.5 * np.sin(2 * np.pi * 50 * t)  # 50Hz纹波  
noise = 0.2 * np.random.normal(0, 1, size=len(t))  # 随机噪声  
input_signal = dc_signal + ripple + noise  # 合成信号  
  
# 方法1：自定义一阶低通滤波器  
class LowPassFilter:  
    def __init__(self, fc, fs):  
        self.fc = fc  
        self.fs = fs  
        self.alpha = 1 / (1 + (fs / (2 * np.pi * fc)))  
        self.y_prev = 0  
  
	def filter(self, x):  
        self.y = self.alpha * x + (1 - self.alpha) * self.y_prev  
        self.y_prev = self.y  
        return self.y  
  
lpf1 = LowPassFilter(fc, fs)  
output_signal1 = np.array([lpf1.filter(x) for x in input_signal])  
  
# 方法2：使用scipy.signal库  
b, a = butter(N=1, Wn=fc/(fs/2), btype='low')  
output_signal2 = lfilter(b, a, input_signal)  
  
# 绘制输入和输出信号  
plt.figure(figsize=(12, 6))  
plt.subplot(2, 1, 1)  
plt.plot(t, input_signal, label='Input Signal')  
plt.plot(t, output_signal1, label='Output Signal (Custom LPF)')  
plt.legend()  
plt.title('Custom Low Pass Filter')  
  
plt.subplot(2, 1, 2)  
plt.plot(t, input_signal, label='Input Signal')  
plt.plot(t, output_signal2, label='Output Signal (SciPy LPF)')  
plt.legend()  
plt.title('SciPy Low Pass Filter')  
  
plt.xlabel('Time [s]')  
plt.tight_layout()  
plt.show()

运行结果：

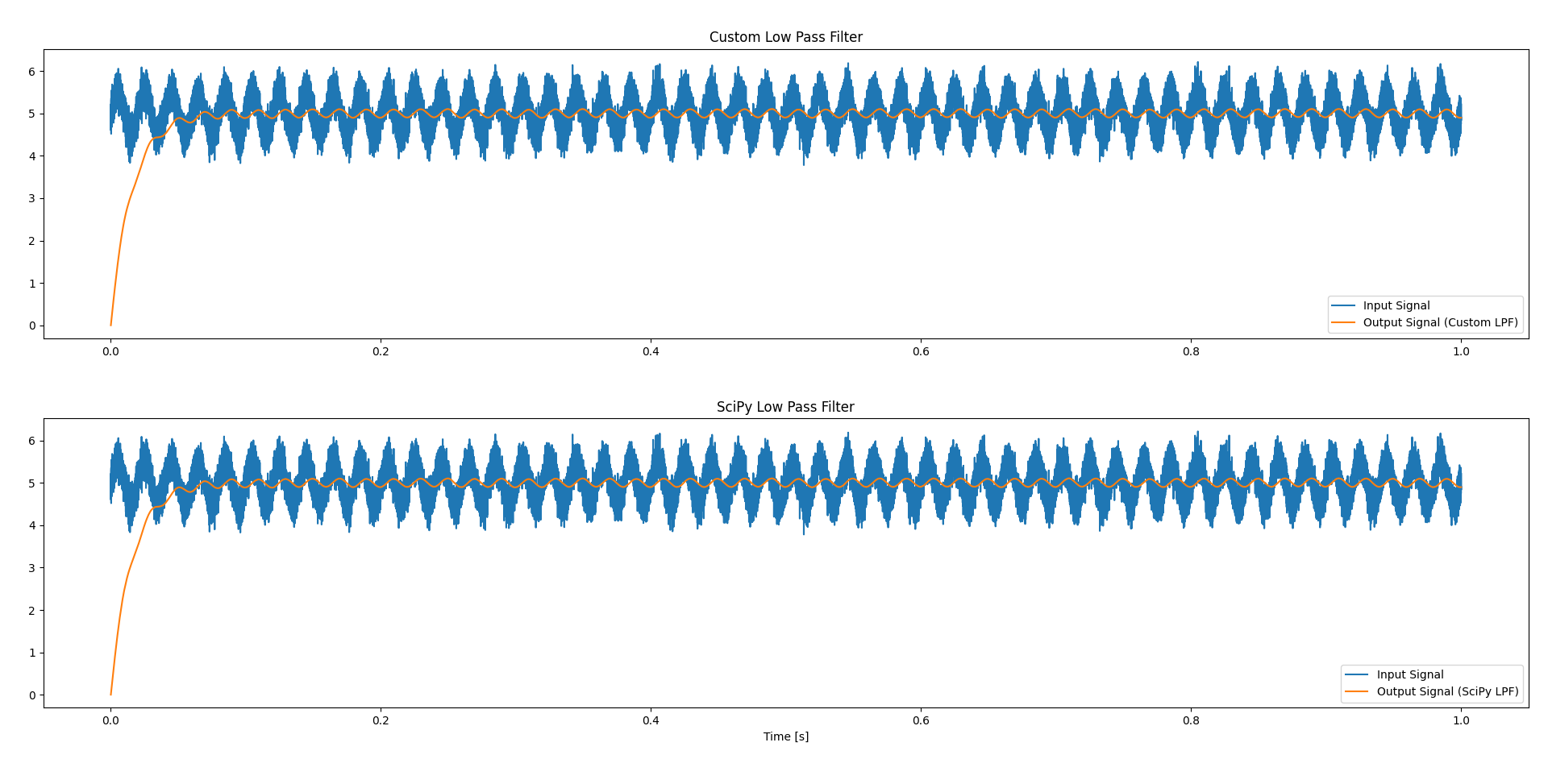
可以看到，结果基本一致，说明滤波器设计的没有问题。

软件一阶低通滤波器绘制Bode图

还没写完

双线性变换法

上面讲的都是后向差分法，下面讲下使用双线性变化对一阶滤波器进行离散化。

双线性变换法是一种更为精确的离散化方法，它通过将 (s) 平面映射到 (z) 平面的一个特定区域（通常是单位圆内），来避免频率混叠和稳定性问题。双线性变换法的公式较为复杂，通常用于需要较高精度和稳定性的场合。

首先，我们有一阶低通滤波器在连续时间域中的传递函数： \[ H(s) = \frac{1}{\tau s + 1} \] 其中，$\tau$ 是时间常数，$s$ 是连续时间域的复频率变量。

为了将这个连续时间滤波器转换为离散时间滤波器，我们使用双线性变换。双线性变换是一种将$s$平面映射到$z$平面的方法，其映射关系为：

\[ s = \frac{2}{T} \frac{1 - z^{-1}}{1 + z^{-1}} \]

其中，$T$ 是采样周期，$z$ 是离散时间域的复频率变量。

现在，我们将上述$s$的表达式代入连续时间滤波器的传递函数$H(s)$中：

\[ H(z) = \frac{1}{\tau \frac{2}{T} \frac{1 - z^{-1}}{1 + z^{-1}} + 1} \]

化简得：

\[ H(z) = \frac{T}{2\tau} \frac{1 + z^{-1}}{1 + \frac{T}{2\tau} (1 - z^{-1})} \]

进一步化简为：

\[ H(z) = \frac{T}{2\tau + T} \frac{1 + z^{-1}}{1 - \frac{2\tau - T}{2\tau + T} z^{-1}} \]

现在，我们已经得到了离散时间滤波器的传递函数$H(z)$。接下来，我们需要将这个传递函数转换为差分方程的形式。

根据 $H(z)$ 的表达式，我们有：

\[ Y(z) = H(z) X(z) \]

\[ Y(z) = \frac{T}{2\tau + T} \frac{1 + z^{-1}}{1 - \frac{2\tau - T}{2\tau + T} z^{-1}} X(z) \]

为了将上式转换为时域中的差分方程，我们需要使用$z$变换的性质。具体地，我们知道：

\[ y(n) = Y(z) \Big|_{z=e^{j\omega T}} \]

\[ x(n) = X(z) \Big|_{z=e^{j\omega T}} \]

并且，对于任意函数 $f(n)$ ，有：

\[ f(n-1) = z^{-1} F(z) \Big|_{z=e^{j\omega T}} \]

应用这些性质，我们可以将$Y(z)$的表达式转换为时域中的差分方程：

\[ y(n) = \frac{T}{2\tau + T} \left[ x(n) + x(n-1) \right] + \frac{2\tau - T}{2\tau + T} y(n-1) \]

为了将上式写得更标准一些，我们可以将系数进行整理：

\[ a_1 = \frac{2\tau - T}{2\tau + T} \]

\[ b_0 = \frac{T}{2\tau + T} \]

\[ b_1 = \frac{T}{2\tau + T} \]

这样，我们就得到了一阶低通滤波器的离散时间实现形式：

\[ y(n) = a_1 \cdot y(n-1) + b_0 \cdot x(n) + b_1 \cdot x(n-1) \]

其中，$y(n)$ 是当前输出，$y(n-1)$ 是上一次输出，$x(n)$ 是当前输入，$x(n-1)$ 是上一次输入。系数$a_1$、$b_0$和$b_1$由采样周期$T$和时间常数$\tau$决定。

带入 $\tau$

将 $\tau = \frac{1}{2\pi f_c}$ 带入之前得到的差分方程参数中，我们可以重写这些参数。

现在，将 $\tau = \frac{1}{2\pi f_c}$ 代入上述参数中：

\[ a_1 = \frac{2 \cdot \frac{1}{2\pi f_c} - T}{2 \cdot \frac{1}{2\pi f_c} + T} = \frac{1 - \pi f_c T}{\pi f_c T + 1} \]

\[ b_0 = \frac{T}{2 \cdot \frac{1}{2\pi f_c} + T} = \frac{\pi f_c T}{\pi f_c T + 1} \]

\[ b_1 = \frac{T}{2 \cdot \frac{1}{2\pi f_c} + T} = \frac{\pi f_c T}{\pi f_c T + 1} \]

因此，差分方程可以写为：

\[ y(n) = \frac{1 - \pi f_c T}{\pi f_c T + 1} \cdot y(n-1) + \frac{\pi f_c T}{\pi f_c T + 1} \cdot x(n) + \frac{\pi f_c T}{\pi f_c T + 1} \cdot x(n-1) \]

这样，我们就得到了用截止频率 $f_c$ 和采样周期 $T$ 表示的一阶低通滤波器的差分方程。

一阶高通滤波器（HPF）

一阶高通滤波器则允许高频信号通过，而抑制低频信号。其设计和低通滤波器类似，但电路的连接方式有所不同。

设计

设计一阶高通滤波器时，同样需要确定截止频率。高通滤波器的电阻和电容连接方式与低通滤波器不同，以实现高频信号的通过和低频信号的衰减。

传递函数

一阶高通滤波器的传递函数可以表示为：

\[ H(s) = \frac{s\tau}{1 + s\tau} \]

与低通滤波器类似，$s$ 是复频率，$\tau$ 是时间常数。这个传递函数描述了滤波器对不同频率信号的响应特性。

陷波滤波器

陷波滤波器（Notch Filter）简介

陷波滤波器是一种特殊的滤波器，用于在特定频率处抑制信号，即在该频率处形成一个“陷波”（notch），使得该频率的信号通过滤波器后大幅衰减。陷波滤波器在信号处理中常用于去除噪声、抑制干扰等场景。

陷波滤波器的主要参数包括： - 陷波中心频率（$\omega_{c}$）：滤波器抑制信号的中心频率。 - 陷波宽度（$\omega_{b}$）：陷波区域的宽度，通常定义为衰减到-3dB时的频率差值。 - 陷波深度（depth）：中心频率处的衰减倍数。

双线性变换离散化过程

双线性变换是一种将连续时间系统（s域）转换为离散时间系统（z域）的常用方法。其本质是一种数值积分法，采用梯形方法来近似计算积分。

二阶陷波滤波器的连续时间传递函数为：

\[ G(s) = \frac{s^2 + \omega_{c}^2}{s^2 + \omega_{b}s + \omega_{c}^2} \]

其中，$s$ 是连续时间复频率变量，$\omega_{c}$ 是陷波中心频率，$\omega_{b}$ 是陷波宽度。

双线性变换是一种将$s$平面映射到$z$平面的方法，其映射关系为：

\[ s = \frac{2}{T} \frac{1 - z^{-1}}{1 + z^{-1}} \]

其中，$T$ 是采样周期，$z$ 是离散时间域的复频率变量。

将双线性变换公式代入原始传递函数，得到：

\[ G(z)=\frac{z^{-2}\left(T^{2} \omega_{c}^{2}+4\right)+z^{-1}\left(2 T^{2} \omega_{c}^{2}-8\right)+T^{2} \omega_{c}^{2}+4}{z^{-2}\left(T^{2} \omega_{c}^{2}-2 \omega_{b} T+4\right)+z^{-1}\left(2 T^{2} \omega_{c}^{2}-8\right)+T^{2} \omega_{c}^{2}+2 T \omega_{b}+4} \]

进一步化简，得到：

\[ G(z) = \frac{a_0 + a_1z^{-1} + a_2z^{-2}}{b_0 + b_1z^{-1} + b_2z^{-2}} \]

其中， - $a_0 = T^{2} \omega_{c}^{2}+4$ - $a_1 = 2 T^{2} \omega_{c}^{2}-8$ - $a_2 = T^{2} \omega_{c}^{2}+4 = a_0$ - $b_0 = T^{2} \omega_{c}^{2}+2 T \omega_{b}+4$ - $b_1 = 2 T^{2} \omega_{c}^{2}-8 = a_1$ - $b_2 = T^{2} \omega_{c}^{2}-2 \omega_{b} T+4$

根据离散化后的传递函数，可以写出差分方程：

\[ c(n) = \frac{a_0}{b_0}r(n) + \frac{a_1}{b_0}r(n-1) + \frac{a_2}{b_0}r(n-2) - \frac{b_1}{b_0}c(n-1) - \frac{b_2}{b_0}c(n-2) \]

其中，$c(n)$ 是第 $n$ 次输出信号，$r(n)$ 是第 $n$ 次输入信号。

代码

import numpy as np  
import matplotlib.pyplot as plt  
# from scipy.signal import lfilter  
  
# 参数设置  
fs = 45000/8  # 采样频率（Hz）  
T = 2.0   # 信号时长（s）  
t = np.linspace(0, T, int(fs*T), endpoint=False)  # 时间向量  
  
# 输入信号  
dc_level = 8.0  # 直流量（A）  
ripple_50Hz = 1 * np.sin(2 * np.pi * 50 * t)  # 50Hz纹波分量（A）  
ripple_70Hz = 1 * np.sin(2 * np.pi * 70 * t)  # 70Hz纹波分量（A）  
ripple_22500Hz = 0.25 * np.sin(2 * np.pi * 22500 * t)  # 22.5kHz纹波分量（A）  
ripple_140000Hz = 0.1 * np.sin(2 * np.pi * 140000 * t)  # 140kHz纹波分量（A）  
input_signal = dc_level + ripple_50Hz + ripple_70Hz
  
# 陷波滤波器参数  
wc = 2 * np.pi * 50  # 陷波中心频率（rad/s）  
wb = 2 * np.pi * 10  # 陷波宽度（rad/s）  
Ts = 1/fs  # 采样时间（s）  
  
# 离散化后的陷波滤波器系数  
a0 = 4 + wc**2 * Ts**2  
a1 = 2 * Ts**2 * wc**2 - 8  
a2 = a0  
b0 = 4 + wc**2 * Ts**2 + 2 * wb * Ts  
b1 = 2 * Ts**2 * wc**2 - 8  
b2 = 4 + wc**2 * Ts**2 - 2 * wb * Ts  

# 打印系数值  
print(f"a0 = {a0}")  
print(f"a1 = {a1}")  
print(f"a2 = {a2}")  
print(f"b0 = {b0}")  
print(f"b1 = {b1}")  
print(f"b2 = {b2}")  
  
# 打印系数与b0的比值  
print(f"a0/b0 = {a0/b0}")  
print(f"a1/b0 = {a1/b0}")  
print(f"a2/b0 = {a2/b0}")  
print(f"b1/b0 = {b1/b0}")  
print(f"b2/b0 = {b2/b0}")

# 打印系数与b0的比值  
print(f"Q15: a0/b0 = {(a0/b0)*(2**15)}")  
print(f"Q15: a1/b0 = {(a1/b0)*(2**15)}")  
print(f"Q15: a2/b0 = {(a2/b0)*(2**15)}")  
print(f"Q15: b1/b0 = {(b1/b0)*(2**15)}")  
print(f"Q15: b2/b0 = {(b2/b0)*(2**15)}")

# 初始化输出信号数组  
output_signal = np.zeros_like(input_signal)  

# 应用陷波滤波器  
# output_signal = lfilter([a0, a1, a2], [b0, b1, b2], input_signal)  

# 应用差分方程进行滤波  
# 注意：这里我们假设初始条件为0（即y[-1] = y[-2] = 0）  
for k in range(2, len(input_signal)):  
    output_signal[k] = (a0*input_signal[k] + a1*input_signal[k-1] + a2*input_signal[k-2] -  
                        b1*output_signal[k-1] - b2*output_signal[k-2]) / b0  

  
# 绘制输入输出信号  
plt.figure(figsize=(10, 6))  
plt.subplot(2, 1, 1)  
plt.plot(t, input_signal)  
plt.title('Input Signal')  
plt.xlabel('Time (s)')  
plt.ylabel('Amplitude (A)')  
  
plt.subplot(2, 1, 2)  
plt.plot(t, output_signal)  
plt.title('Output Signal')  
plt.xlabel('Time (s)')  
plt.ylabel('Amplitude (A)')  
  
plt.tight_layout()  
plt.show()

运行结果：

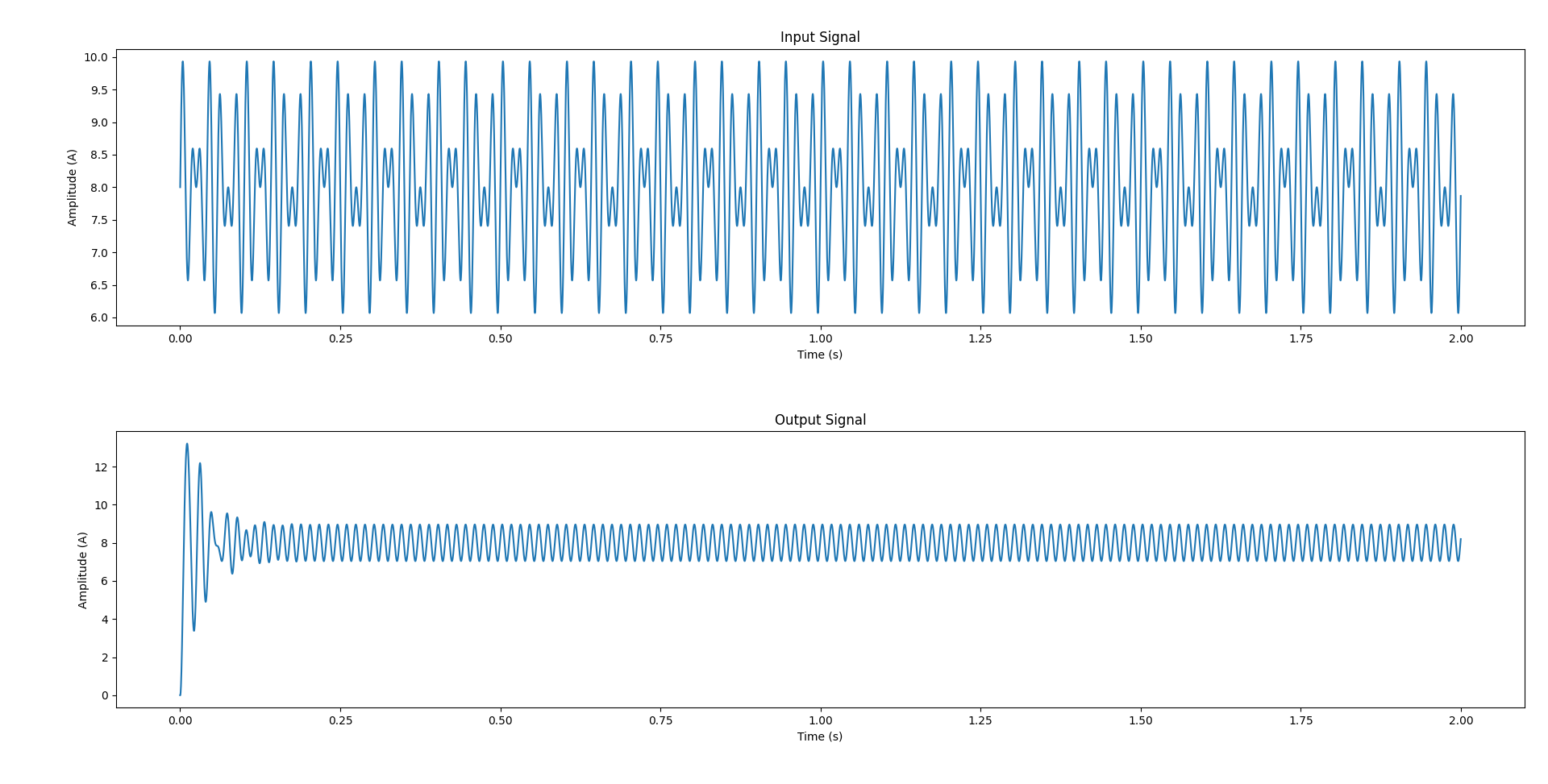
可以看到，滤波器只滤除了50Hz的成分，保留了70Hz的成分。

生成gif

import numpy as np  
import matplotlib.pyplot as plt  
from matplotlib.animation import FuncAnimation  
  
# 参数设置  
fs = 45000 / 8  # 采样频率（Hz）  
T = 2.0  # 信号时长（s）  
t = np.linspace(0, T, int(fs * T), endpoint=False)  # 时间向量  
  
# 输入信号  
dc_level = 8.0  # 直流量（A）  
ripple_50Hz = 1 * np.sin(2 * np.pi * 50 * t)  # 50Hz纹波分量（A）  
input_signal = dc_level + ripple_50Hz  
  
# 初始化输出信号数组  
output_signal = np.zeros_like(input_signal)  
  
# 设置GIF图像的帧  
frames = []  
  
# 定义更新函数，用于生成每一帧的图像  
def update(frame):  
    wc = 2 * np.pi * (40 + frame * (60 - 40) / 100)  # 陷波中心频率从40Hz变化到60Hz  
    wb = 2 * np.pi * 10  # 陷波宽度（rad/s）  
    Ts = 1 / fs  # 采样时间（s）  
  
    # 离散化后的陷波滤波器系数  
    a0 = 4 + wc ** 2 * Ts ** 2  
    a1 = 2 * Ts ** 2 * wc ** 2 - 8  
    a2 = a0  
    b0 = 4 + wc ** 2 * Ts ** 2 + 2 * wb * Ts  
    b1 = 2 * Ts ** 2 * wc ** 2 - 8  
    b2 = 4 + wc ** 2 * Ts ** 2 - 2 * wb * Ts  
  
    # 应用差分方程进行滤波  
    # 注意：这里我们假设初始条件为0（即y[-1] = y[-2] = 0）  
    for k in range(2, len(input_signal)):  
        output_signal[k] = (a0 * input_signal[k] + a1 * input_signal[k - 1] + a2 * input_signal[k - 2] -  
                            b1 * output_signal[k - 1] - b2 * output_signal[k - 2]) / b0  
  
    # 绘制图像  
    plt.clf()  
    plt.plot(t, input_signal, label='Input Signal')  
    plt.plot(t, output_signal, label='Output Signal')  
    plt.title(f'Center Frequency: {wc / (2 * np.pi):.2f} Hz')  
    plt.xlabel('Time (s)')  
    plt.ylabel('Amplitude (A)')  
    plt.legend()  
  
# 生成GIF图像  
fig, ax = plt.subplots(figsize=(10, 6))  
anim = FuncAnimation(fig, update, frames=np.arange(0, 101, 1), interval=100, blit=False)  
anim.save('notch_filter.gif', writer='imagemagick')  
  
plt.show()

三参数的陷波滤波器

即陷波深度可调的陷波滤波器。

三参数的陷波滤波器的连续时间传递函数为：

\[ G(s) = \frac{s^2 + 2 k_2 \omega_{c} s + \omega_{c}^2}{s^2 + 2 k_1 \omega_{c} s + \omega_{c}^2} \]

其中，$\omega_{c}$ 是陷波频率，$k_1$ 和 $k_2$ 是阻尼比的系数。

双线性变换：

\[ G(s)=\frac{4+4 k_{2} \omega_{c} T_{s}+\omega_{c}^{2} T_{s}^{2}+\left(2 \omega_{c}^{2} T_{s}^{2}-8\right) z^{-1}+\left(\omega_{c}^{2} T_{s}^{2}-4 k_{2} \omega_{c} T_{s}+4\right) z^{-2}}{4+4 k_{1} \omega_{c} T_{s}+\omega_{c}^{2} T_{s}^{2}+\left(2 \omega_{c}^{2} T_{s}^{2}-8\right) z^{-1}+\left(\omega_{c}^{2} T_{s}^{2}-4 k_{1} \omega_{c} T_{s}+4\right) z^{-2}} \]

其中， - $a_0 = 4+4 k_{2} \omega_{c} T_{s}+\omega_{c}^{2} T_{s}^{2}$ - $a_1 = 2 \omega_{c}^{2} T_{s}^{2}-8$ - $a_2 = \omega_{c}^{2} T_{s}^{2}-4 k_{2} \omega_{c} T_{s}+4$ - $b_0 = 4+4 k_{1} \omega_{c} T_{s}+\omega_{c}^{2} T_{s}^{2}$ - $b_1 = 2 \omega_{c}^{2} T_{s}^{2}-8$ - $b_2 = \omega_{c}^{2} T_{s}^{2}-4 k_{1} \omega_{c} T_{s}+4$

\[ b_{0} Y(z)+b_{1} Y(z-1)+b_{2} Y(z-2)=a_{0} X(z)+a_{1} X(z-1)+a_{2} X(z-2) \]

根据离散化后的传递函数，可以写出差分方程：

\[ c(n) = \frac{a_0}{b_0}r(n) + \frac{a_1}{b_0}r(n-1) + \frac{a_2}{b_0}r(n-2) - \frac{b_1}{b_0}c(n-1) - \frac{b_2}{b_0}c(n-2) \]

其中，$c(n)$ 是第 $n$ 次输出信号，$r(n)$ 是第 $n$ 次输入信号。可以发现和上面的两参数的陷波滤波器形式是一致的。

三参数陷波滤波器是一种特殊类型的带阻滤波器，其特点在于可以独立调整陷波中心频率、陷波深度（即中心频率处的衰减倍数）和陷波带宽（衰减到-3dB时的频率差值）。双线性变换法是将模拟滤波器转换为数字滤波器的一种常用方法，特别适用于处理模拟滤波器到数字滤波器的转换过程中的频率畸变问题。以下是对三参数陷波滤波器的双线性变换的详细介绍：

陷波滤波器的三个参数：

陷波中心频率（$\omega_c$）：这是滤波器需要“陷掉”的频率点，也是陷波效果最明显的频率。
陷波深度（depth）：表示在陷波中心频率处信号的衰减倍数。陷波深度越大，表示该频率点的信号被衰减得越厉害。
陷波带宽（$\omega_b$）：表示陷波效果显著的频率范围宽度，即衰减到-3dB时的频率差值。

由此我们得出两个重要公式：

\[ \large k_{1}=\sqrt{\frac{\left(1-\sqrt{1+\frac{\omega_{s}^{2}}{\omega_{c}^{2}}}\right)}{4 \cdot \operatorname{depth}^{2}-2}} \quad \quad k_{2}=\operatorname{depth} \cdot k_{1} \]

matlab代码：

% 定义陷波滤波器的参数    
fc = 100;         % 陷波频率 (Hz)    
depth = 0.01;     % 陷波深度衰减100倍，范围[-0.707, 0.707]    
Wn = 2 * pi * fc; % 陷波频率 (rad/s)    
fbw = 40;         % 带宽 (Hz)    
B = 2 * pi * fbw; % 带宽 (rad/s)    
fs = 1000;        % 采样频率 (Hz)    
Ts = 1 / fs;      % 采样周期 (s)    
    
% 计算阻尼比 zeta1 和 zeta2    
zeta1 = sqrt((-sqrt(B^2 / (Wn^2) + 1) + 1) / (4 * depth^2 - 2));    
zeta2 = zeta1 * depth;    
    
% 创建离散时间传递函数 H    
numerator = [4 + Wn^2 * Ts^2 + 4 * zeta2 * Wn * Ts, 2 * Wn^2 * Ts^2 - 8, 4 - 4 * Wn * zeta2 * Ts + Wn^2 * Ts^2];    
denominator = [4 + Wn^2 * Ts^2 + 4 * zeta1 * Wn * Ts, 2 * Wn^2 * Ts^2 - 8, 4 - 4 * Wn * zeta1 * Ts + Wn^2 * Ts^2];    
H = tf(numerator, denominator, Ts);    
    
% 将离散系统转换为连续系统    
Hc = d2c(H, 'tustin');    
    
% 设置Bode图选项    
P = bodeoptions;    
P.Grid = 'on';         % 显示网格    
P.FreqUnits = 'Hz';    % 频率单位为Hz    
    
% 绘制Bode图    
bode(Hc, P);

一阶低通滤波器

一阶低通滤波器（LPF）

传递函数

一阶RC低通滤波电路的传递函数

截止频率公式

时域微分方程

软件滤波器

滤波系数 $ a $ 的计算公式

代码

软件一阶低通滤波器

一阶低通滤波器，截止频率，Bode图

与python库对比

软件一阶低通滤波器绘制Bode图

双线性变换法

带入 \(\tau\)

一阶高通滤波器（HPF）

设计

传递函数

陷波滤波器

陷波滤波器（Notch Filter）简介

双线性变换离散化过程

代码

生成gif

三参数的陷波滤波器